Matematikë, Lëndët e Përgjithshme A 2012
Pyetja 1
Nëse
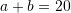 dhe
dhe 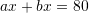 . Sa është vlera e
. Sa është vlera e  – it ?
– it ?A.

B.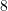
C.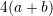
D.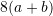
Zgjidhje:
Nga
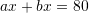
Kemi,
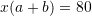
Dimë se
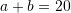
Kemi,
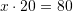
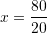
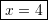
Pyetja 2
Nëse
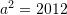 , sa është vlera e shprehjes
, sa është vlera e shprehjes 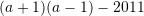 ?
?A.
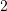
B.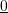
C.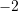
D.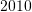
Zgjidhje:
Nga
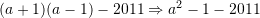
Zëvendësojmë
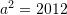
Kemi,
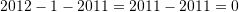
Pyetja 3
Është dhënë ekuacioni
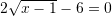 . Sa është vlera e
. Sa është vlera e 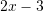 ?
?A. 10
B. 13
C. 15
D. 17Zgjidhje:
Gjejmë
 -in nga ekuacioni
-in nga ekuacioni 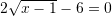
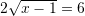
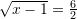
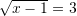 /
/
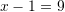
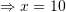
Kështu,
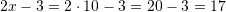
Pyetja 4
Nëse
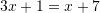 dhe
dhe 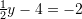 . Sa është vlera e
. Sa është vlera e 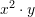 ?
?A. 12
B. 24
C. 36
D. 48Zgjidhje:
Gjejmë
 nga
nga 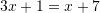
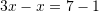
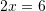
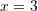
Gjejmë
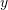 nga
nga 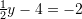
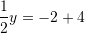
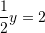
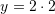
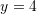
Kështu,
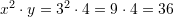
Pyetja 5
Cila është moda për të dhënat vijuese
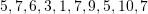 ?
?A.
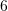
B.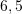
C.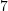
D.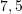
Modë është karakteristika e cila ka frekuencëmë të lartë (karakteristika e cila përseritet më së shpeshti).
Pyetja 6
Një lokal ka syprinën
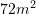 . Syprina rritet edhe për
. Syprina rritet edhe për 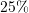 . Sa
. Sa 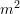 do t’i ketë lokali?
do t’i ketë lokali?A.
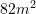
B.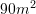
C.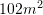
D.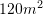
Zgjidhje:
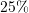 e
e 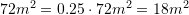
Pra, syprina rritet për
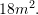
Gjithsej, lokali do t’i ketë
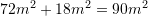
Pyetja 7
Nëse
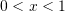 , cili nga pohimet është i saktë ?
, cili nga pohimet është i saktë ?I.
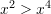 II.
II. 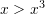 III.
III. 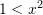
A. I. dhe II.
B. Vetëm I.
C. Vetëm II.
D. Vetëm III.Zgjidhje:
Pasi qe
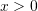 , pjestojme
, pjestojme 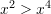 ane per ane me
ane per ane me 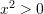 , si dhe
, si dhe 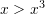 pjestojme me
pjestojme me 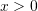 ,
,Atehere, kemi jobarazime identike
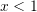
Pra, vlen
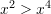 dhe
dhe 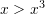 .
.Poashtu vlenë edhe
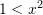 mirepo jo vetem
mirepo jo vetem 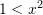
Pyetja 8
Sa është shuma e 100 numrave të parë natyrorë?
A. S =1000
B. S = 5000
C. S = 5050
D. S = 5500Zgjidhje:
Kërkohet të gjendet shuma e vargut aritmetik
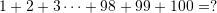
Shfrytëzojmë formulë për shumën e
 -termave
-termave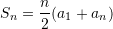
Në rastin tonë,
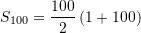
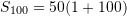
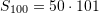
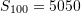
Pyetja 9
Sa është vlera e shprehjes
![Rendered by QuickLaTeX.com \displaystyle{M=64\cdot\left(\frac{1}{2}\right)^5+\sqrt[3]{27}:3+(-1)^5\cdot\frac{27}{3}+(-2)^2}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-289aa1e6ec5a1cc1942ee7f9604fd26b_l3.png) ?
?A.
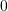
B.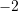
C.
D.![Rendered by QuickLaTeX.com \sqrt[3]{3}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-3598f8df5a2e1319a7a69f96813a4cb4_l3.png)
Zgjidhje:
![Rendered by QuickLaTeX.com M=64\cdot\left(\frac{1}{32}\right)+\sqrt[3]{27}:3+(-1)^5\cdot\frac{27}{3}+(-2)^2](https://testimatures.com/wp-content/ql-cache/quicklatex.com-c61910acd1c51844230c802d26857cf4_l3.png)
![Rendered by QuickLaTeX.com M=2+\sqrt[3]{27}:3+(-1)^5\cdot\frac{27}{3}+(-2)^2](https://testimatures.com/wp-content/ql-cache/quicklatex.com-f0ca4a71ac5b0b4f39085ce4248a6dbd_l3.png)
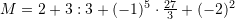
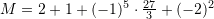
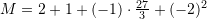
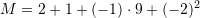
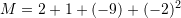
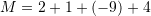
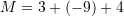
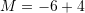
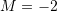
Pyetja 10
Sa është perimetri i figurës së dhënë, nëse
![Rendered by QuickLaTeX.com c =[A,B]=13cm, s=[E, D]=5cm](https://testimatures.com/wp-content/ql-cache/quicklatex.com-7aad98d36f4af65a64db611ce5bb6e68_l3.png) dhe
dhe ![Rendered by QuickLaTeX.com [C, D]=\frac{7b}{6}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-9da0ee93b13cff28ebc17b35331567c6_l3.png) ?
?A.
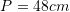
B.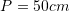
C.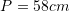
D.
Zgjidhje:
Së pari gjejmë brinjen
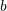 te trekendëshit ABC me anen e Teoremes se Pitagores
te trekendëshit ABC me anen e Teoremes se Pitagores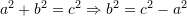
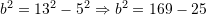
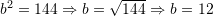
Keshtu perimetri i figures eshte:
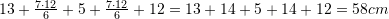
Pyetja 11
Për transportimin e një sasie të thëngjillit nevojiten 24 kamionë me fuqi transportuese 14 tonëshe. Sa kamionë me fuqi bartëse 16 tonëshe do të ishin të nevojshëm për transportimin e sasisë së njëjtë të thëngjillit?
A. 21
B. 23
C. 17
D. 19Zgjidhje:
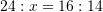
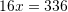
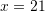
Pyetja 12
Sa është vlera e shprehjes
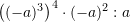 ?
?A.
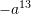
B.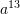
C.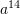
D.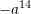
Zgjidhje:
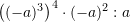
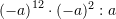
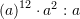
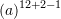
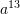
Pyetja 13
Cili funksion i përgjigjet grafikut të dhënë ?
A.
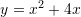
B.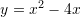
C.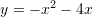
D.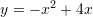
Zgjidhje:
Meqë grafiku i dhënë është parabolë, caktojmë zerot dhe kulmin e parabolës për funskionin
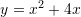 .
.Zerot e funksionit
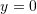 nëse
nëse 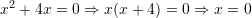
Kulmi i parabolës
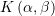 , ku
, ku 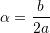 dhe
dhe 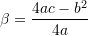
Rrjedhimisht
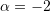 dhe
dhe 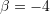 .
.Pra, zerot dhe kulmi i parabolës i përgjigjen grafikut të funksionit
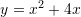 .
.Pyetja 14
Një kopsht ka formën e drejtëkëndshit me syprinë 2 300 m . Cili ekuacion kuadratik i përgjigjet që zgjidhjet e tij mundësojnë që kopshti të rrethohet me një tel të gjatë 74m?
A.
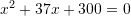
B.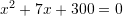
C.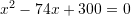
D.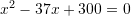
Zgjidhje:
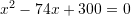
Gjejmë zgjidhjet e ekuacionit
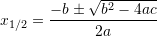
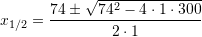
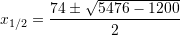
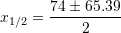
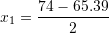
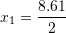
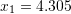
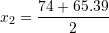
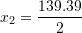
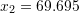
Shuma e zgjidhjeve është
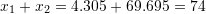
Pyetja 15
Sa është shuma e zgjidhjeve të sistemit të ekuacioneve:
 ?
?A.
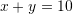
B.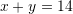
C.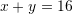
D.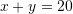
Zgjidhje:
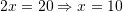
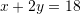
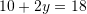
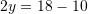
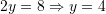
Shuma e zgjidhjeve është
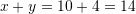
Pyetja 16
Nëse
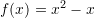 dhe
dhe 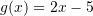 , sa është
, sa është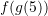 ?
?A. 10
B. 15
C. 20
D. 25Zgjidhje:
Së pari gjejmë
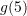
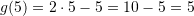
Tani,
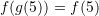
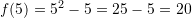
Pyetja 17
Në figurën e dhënë pika
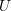 është ndërmjet pikave
është ndërmjet pikave 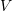 dhe
dhe 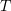 . Nëse
. Nëse 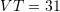 njësi matëse, sa është gjatësia e segmentit
njësi matëse, sa është gjatësia e segmentit 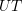 ?
?A.
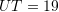
B.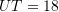
C.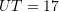
D.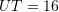
Zgjidhje:
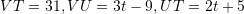
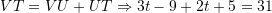
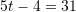
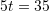
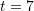
Keshtu,
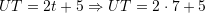
Pra,
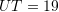
Pyetja 18
Sa është shuma e numrave kompleks
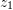 e
e 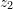 të paraqitur në figurë ?
të paraqitur në figurë ?A.
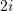
B.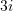
C.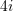
D.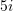
Zgjidhje:
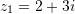
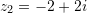
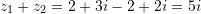
Pra,
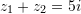
Pyetja 19
Vija në diagram tregon temperaturën mesatare ditore gjatë një jave në Kosovë. Sa është temperatura mesatare e javës e shprehur në Celsius?
A.
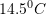
B.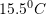
C.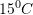
D.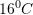
Zgjidhje:
Ne baze te diagramit temperatura per diten e hene, marte, merkure, enjte, premte, shtune dhe diele jane
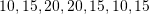 perkatesisht.
perkatesisht.Temperatura mesatare e javes eshte:
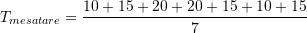
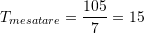
Pyetja 20
Është dhënë bashkësia e numrave
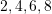 . Sa numra dyshifrorë natyrorë mund të formohen prej tyre ashtu që shifrat mos të përsëriten ?
. Sa numra dyshifrorë natyrorë mund të formohen prej tyre ashtu që shifrat mos të përsëriten ?A. 6
B. 12
C. 16
D. 20Zgjidhje:
Ketu kemi te bejme me variacione te klases se dyte prej 4 elementeve.
Pra,
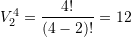
Pyetja 21
Cila nga formulat i përgjigjet figurës?
A.
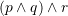
B.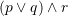
C.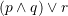
D.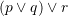
Zgjidhje:
Rryma duhet te kaloje neper
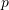 dhe neper
dhe neper 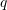 ose vetem neper
ose vetem neper  .
.Prandaj formula e cila i pergjigjet qarkut elektrik eshte
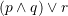
Pyetja 22
Sa është vlera e shprehjes
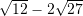 ?
?A.
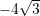
B.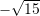
C.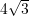
D.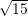 v
vZgjidhje:
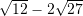
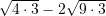
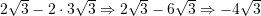
Pyetja 23
Për
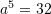 atëherë sa do të jetë
atëherë sa do të jetë 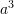 ?
?A.
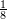
B.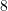
C.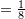
D.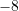
Zgjidhje:
Nga
![Rendered by QuickLaTeX.com a^5=32 \Rightarrow a=\sqrt[5]{32} \Rightarrow a=2](https://testimatures.com/wp-content/ql-cache/quicklatex.com-8f8956ca77241c0a1df04d62c88b08c3_l3.png)
Atëherë
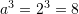
Pyetja 24
Një mall shtrenjtohet për 20 % . Pas disa ditsh lirohet për 20 % . Cila pohim është i saktë?
A. Kthehet në çmimin fillestar.
B. Kthehet në çmimin më të lartë se ai fillestar.
C. Kthehet në çmimin më të ultë se ai fillestar.
D. Kthehet në çmimin për 2% më të lartë se ai fillestar.Pyetja 25
Cili ekuacion i përgjigjet fjalisë “Shuma e zgjidhjeve është 5 ndërsa prodhimi i tyre 6 ” ?
A.
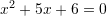
B.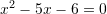
C.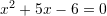
D.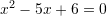
Zgjidhje:
Ekuacioni kuadratik i trajtes se pergjithshme ka formen
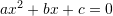 , ku
, ku 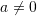
Vlejne keto veti te zgjdhjeve te ekuacionit kuadratik
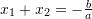 dhe
dhe 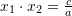
Sepse
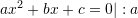
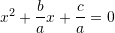
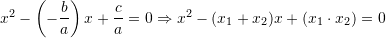
Ne rastin tone,
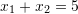
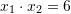
Zevendesojme ne
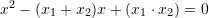
Kemi
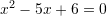
Pyetja 26
Cili transformim gjeometrik është paraqitur në figurë ?
A. Rotacionin
B. Tenslacion
C. Simetrinë qëndrore
D. Simetrinë boshtorePyetja 27
Në rrethin me diametër
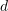 është brendashkruar katrori.
është brendashkruar katrori.
Sa ëshë syprina e katrorit ?A.
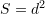
B.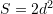
C.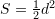
D.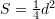
Zgjidhje:
Diagonalja e katrorit te brendashkruar eshte e barabarte me diametrin
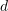 te rrethit.
te rrethit.Ne baze te teoremes se Pitagores
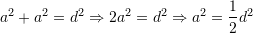
Pra, syprina e katrorit
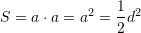
Pyetja 28
Në vargun aritmetik është dhënë
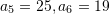 . Sa është
. Sa është 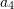 ?
?A.
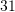
B.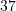
C.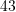
D.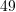
Zgjidhje:
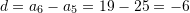
Pra
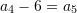
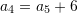
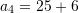
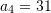
Pyetja 29
Klasa ka
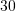 nxënësve , secili prej tyre flet të pakten njëren gjuhë (frangjisht ose anglisht),
nxënësve , secili prej tyre flet të pakten njëren gjuhë (frangjisht ose anglisht), 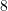 nxënës dijnë vetëm anglisht po aq edhe vetëm frengjisht. Sa nxënës dijnë dy gjuhët ?
nxënës dijnë vetëm anglisht po aq edhe vetëm frengjisht. Sa nxënës dijnë dy gjuhët ?A.
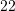
B.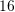
C.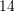
D.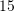
Zgjidhje:
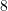 nxënës dijnë vetëm anglisht +
nxënës dijnë vetëm anglisht + 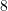 nxënës dijnë vetëm frengjisht = 16
nxënës dijnë vetëm frengjisht = 16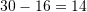
Pyetja 30
Në cilin pikë funksioni
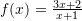 ,
, 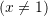 pret boshtin
pret boshtin 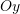 ?
?A.
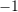
B.
C.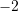
D.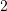
Zgjidhje:
Funksioni
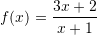 ,
, 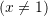 e pret boshtin
e pret boshtin 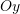 kur
kur 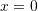 .
.Keshtu,
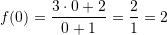
Pra, funksioni
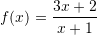 e pret boshtin
e pret boshtin 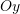 në pikën
në pikën 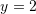 .
.










kto jan do pytje te testit te matures ne matmatik
Pyetja 20, duhet te jete A.6, nuk duhet variacion por kombinacion!
Pergjigja do te ishte 6 vetem nese kerkohet qe te mos llogaritet renditja (psh 24 me 42) qe do te zgjidhej me kombinacion.
Meqenese detyra thote vetem te mos perseriten shifrat e njejta (22, 44, 66, 88) atehere detyra zgjidhet me variacion pa perseritje.
melos duke e pare pytjen e njejt te grupit b drilona ka te drejte
Është dhënë bashkësia e numrave {1, 3, 5, 7}. Sa numra dyshifrorë natyror mund të formohen
prej këtyre numrave në mënyrë që shifrat të mos përsëriten ?
A. 4
B. 6
C. 8
D. 10
vetem zgjidhja 6 eshte e njejt perndryshe 12 nuk eshte
nese ka mundesi drilona na tegon edhe si zgjidhet detyra??
perndryshe zgjidha e detyres qenka
(4) 4! 4*3*2*1 12
——— = ——– = — = 6
(2) 2!*(4-2)! 2*1*2*1 2
perndryshe zgjidha e detyres qenka
(4) n
(2) k
4!
————————=
2!*(4-2)!
4*3*2*1
——- =
2*1*2*1
12/2=6
qetu se aty s dul mir
Po qa po fol palidhje Variacion perdoret kur ska perseritje kombinacioni perdoret per perseritje nese veq mendon pak dhe i hup 1 sec kqyre kemi: 2,4,6,8 regulli sguxojn mu perserit numrat e njejt
24,26,28,42,46,48,62,64,68,82,84,86 mqs patem pak numra perdora metoden e vjeter. Pra jan 12 numra 2 shifror qe kan mund te krijohen nga numrat e dhene nqs sperseriten numri i njejt nese ai regull seshte at’here jan 16 numra.
4! osht 24 se 4*3=12*2=24*1=24/2=12.
$x^2+5x-\sin x$
te pyetja 14 , qysh ka mundsi na me gjet rrenjen e 4276 kur nuk kena kalkulator?
Jipen opcionet edhee e tte gjitha nr i shumzon vet me vetii edhe cila e jep nr 4276 edhe e rrethakon ate nr
a bon dikush nqs nuk priton me na kallxu qka jon KOMBINACIONET , VARIACIONET , dhe PERMUTACIONET dhe qysh zgjidhen ma saktesisht se nuk kom shum njohuri per to :S
Detyra 20 ka rezultatin =6 sepse : 4! 4*3*2*1 24
—- = ———- = —- = 6
(4-2)! (4-2)*(4-2) 2*2
nihere kryhen mbrenda kllapave, 4-2=2 tani 2!=2 , 24/2=12
Shume te veshtira testet a ka marre njeri 10 ?
zgjithne rraja katrore e numrit 559876 sa esht rraja katrore e keti numru?
te detyra e 20 gjith kta persona mos me dit me mledh veq te juu se 4*3*2*1 bajn 24/2 esht 12 .mirr e ka 😀
a ka pytje nga lenda e ed qytetare
bravo bre bal ed qytetare koke i hupt krejt
anii dee ntestt ka pytje edhe nga lenda qytetaree balic 😛
osht i interesun djali me dit ski nevoj me u qartt qe munesh me i ndihmu diqka i ndihmon qe jo se hap gojen shuum
zgjedhja e det.20 esht kshtu {2,4,6,8}={24,26,28,46,48,68,.86,84,82,64,62,42}=numrat nuk perseriten dhe gjithsej jan= 12
detyra e 14 eshte gabim. e para zgjedhja e sakt eshte nen D.
per arsyes me me sgjedhjet e pergjigjes nen D del se x1=25 dhe x2=12.
Atehere perimetri i nje drejtkendeshi ka 2a dhe 2b atehere del se 2*25=50
dhe 2*12=24 ==> 50+24=74.
kurse te zgjedhja nen C do te dilte keshtu x1=4.3 pra 4.3*2=8.6 dhe x2=69.6*2=139.4 ==> 8.6+139.4=148. :D:D
Te pytja e 24 spo kuptoj . p.sh Nje Gje me vler per 10 ero rritet per 20 % behet 12 ero nese zvoglohet per 20 % behet 10.20 cent , Pergjigja eshte gabim , E sakt eshte e D , nese une e kam gabim ju lutem qe te me ndihmoni ne gjetjen e zgjidhjes .
GJON BUZUKU merre 1 vler psh 100$ nese e rrisim per 20% 100$ a bohen 120$ . Tash duhesh me ja zbrit 20% 120$ tash nese ja gjen 120$ 20% (e bon 120/100 qe osht 1.2*20 del 24)del 20% osht 24 e nese e bon 120 – 24 del 96 qe i bjen ma e vogel se vlera e meparshme .
Jo ke bo gabim nkalkulime. Vlera fillestare osht 10 euro dmth rritja e saj per 20% bohet 10+10*.2=12. Masnej 20% i 12 osht 12*.2=2.4, pra 12-2.4=9.6 qe osht ma pak se 10 (qmimi fillestar) 😉
Per ta argumentuar situatën më realisht autori i këtij teksti mbështetet në A.gjuhën e narratorit B.gjuhën e personazheve C.teksti e narratori të jashtëm D.dialogun ndëmjet parsonazheve a ban me mi tregu pergjigjjen e qisajna pytje ne gjuh shqipe nese ka mundesi ok flm
Shkurt pa e lexu tekstin sun e din kerkush , dhe nese osht ajo tekst qe e kam lexuar une pytja e sakt eshte A
Shum emision i qelluem ju pershendet habibi nga svicrra
plzz
kush i din sa pyejtje na kan ra ne test te matures folni ne comment ??