Matematikë, Gjimnazi Matematikë-Informatikë A 2012
Pyetja 1
Sa është vlera e
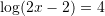 ?
?A.
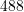
B.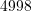
C.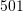
D.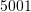
Zgjidhje:
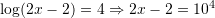
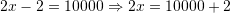
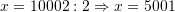
Pyetja 2
Në qoftë se vlenë
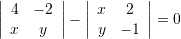 , sa është vlera e
, sa është vlera e  ?
?A. – 2
B. 2
C. -7
D. 8Zgjidhje:
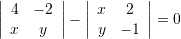
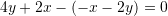
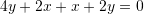
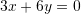
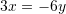
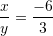
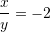
Pyetja 3
Është dhënë funksioni
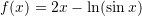 . Sa është
. Sa është 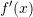 ?
?A.
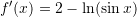
B.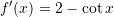
C.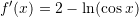
D.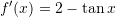
Zgjidhje:
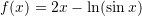
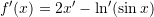
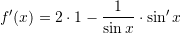
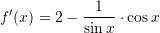
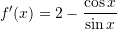
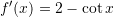
Pyetja 4
Nëse
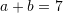 dhe
dhe 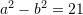 sa është vlera e
sa është vlera e 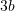 ?
?A.

B.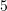
C.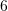
D.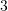
Zgjidhje:
Nga
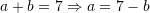
Kemi,
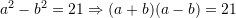
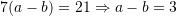
Zëvendësojmë
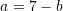
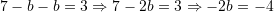
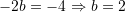
Atëherë
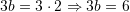
Pyetja 5
Tabela vijuese tregon vlerat e një funksioni
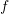 dhe derivatit të tij
dhe derivatit të tij 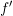 .
.
x f (x) f ‘(x)
0 2 5
1 4 -3
2 -2 3
3 4 2Nëse funksioni
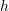 është dhënë me
është dhënë me 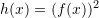 , caktoni
, caktoni 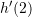 .
.A.
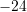
B.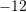
C.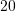
D.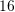
Zgjidhje:
Nga
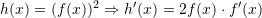
Në rastin tonë
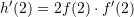
Nga tabela
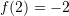 dhe
dhe 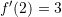
Atëherë
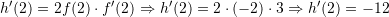
Pyetja 6
Janë dhënë barazimet
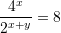 dhe
dhe 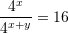 . Sa është vlera e
. Sa është vlera e 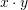 ?
?A. – 2
B. – 4
C. 2
D. 4Zgjidhje:
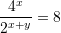
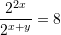
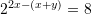
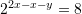
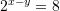
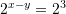
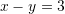
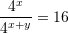
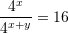
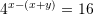
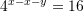
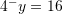
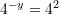
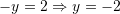
Gjejmë
 -in nga
-in nga 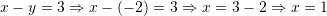
Kështu
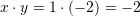
Pyetja 7
Nëse
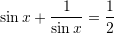 sa është vlera e shprehjes
sa është vlera e shprehjes 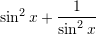
A.

B.
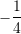
C.
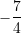
D.

Zgjidhje:
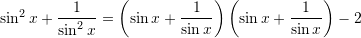
Nga te dhenat e detyres dijme se
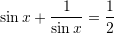
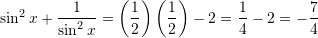
Pyetja 8
Cili është forma kanonike e ekuacionit të hiperbolës nëse
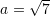 dhe
dhe 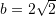 ?
?A.
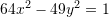
B.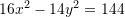
C.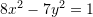
D.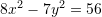
Zgjidhje:
Ekuacioni i hiperbolës në formë kanonike është:
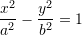
Në rastin tonë, për
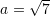 dhe
dhe 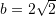 , ekuacioni merr formën
, ekuacioni merr formën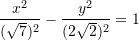
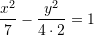
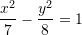
Shumëzojmë ekuacionin me numrin
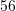
Kemi,
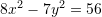
Pra, forma kanonike e ekuacionit të hiperbolës është
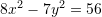
Pyetja 9
Në trekëndëshin ABC, janë dhënë
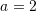 ,
, 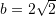 dhe
dhe 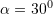 . Zbato teoremen e sinusit dhe trego se cila është vlera e këndit
. Zbato teoremen e sinusit dhe trego se cila është vlera e këndit 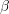 ?
?A.
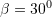
B.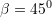
C.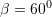
D.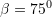
Zgjidhje:
Teorema e Sinusit thotë:
“Në cdo trekëndësh brinjët janë proporcionale me sinuset e këndeve përballë tyre; herësi është i barabartë me diametrin e rrethit të jashtëshkruar në atë trekëndësh.”
Pra,
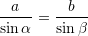
Prej nga,
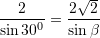
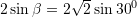
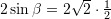
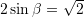
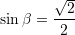

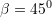
Pyetja 10
Është dhënë funksioni
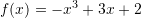 . Cili nga pohimet është i saktë ?
. Cili nga pohimet është i saktë ?A. Funksioni është tek.
B. Funksioni ka asimptotë horizontale.
C. Funksioni ka shkëputje në pikën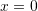 .
.
D. Funksioni ka vlera ekstreme për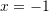 dhe
dhe 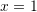
Pyetja 11
Nëse
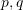 janë zgjidhjet e ekuacionit
janë zgjidhjet e ekuacionit 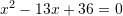 , sa është
, sa është 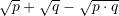 ?
?A. 5
B. 1
C. -1
D. 0Zgjidhje:
Fillimisht gjemë zgjidhjet
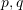
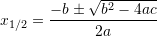
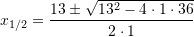
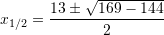
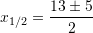
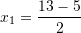
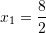
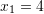
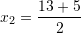
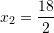
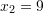
Pra
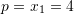 dhe
dhe 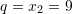
Tani zëvenedësojmë
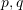 në
në 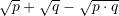
Kemi,
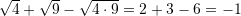
Pyetja 12
Për çfarë vlere të
 -it funksioni
-it funksioni 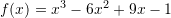 ka vlerë maksimale ?
ka vlerë maksimale ?A. 1
B. 2
C. 3
D. 4Zgjidhje:
Pyetja 13
Në qoftëse
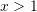 , atëherë cila nga shprehjet e dhëna :
, atëherë cila nga shprehjet e dhëna :I.
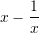
II.
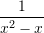
III.
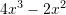
rriten me zmadhimin e
 –it ?
–it ?A. Vetëm I
B. I dhe II
C. I dhe III
D. Vetëm IIIPyetja 14
Sa duhet të jetë vlera e parametrit
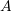 , në ekuacionin e drejtëzës
, në ekuacionin e drejtëzës 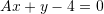 , në mënyrë që kjo drejtëz ta pret boshtin
, në mënyrë që kjo drejtëz ta pret boshtin 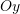 me segment dy herë më të madh se boshtin
me segment dy herë më të madh se boshtin 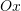 ?
?A. 1
B. 2
C. 4
D. 8Pyetja 15
Cili është domeni i funksionit
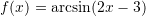 ?
?A.
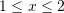
B.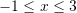
C.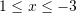
D.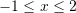
Pyetja 16
Sa është syprina e trekëndëshit i cili formohet prej drejtëzave
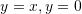 dhe
dhe 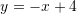 ?
?A.
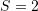
B.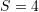
C.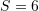
D.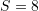
Pyetja 17
Është dhënë shprehja
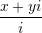 i, ku
i, ku 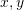 janë numra realë ndërsa
janë numra realë ndërsa  është njësi komplekse. Sa është vlera e
është njësi komplekse. Sa është vlera e 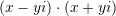 ?
?A. 5
B. 13
C. 17
D. 25Pyetja 18
Sa rrafshe mund të përcaktohen prej 10 pikave nëse jo më shumë se tri pika jokomplanare?
A. 10
B. 30
C. 60
D. 120Pyetja 19
Në hambar ka 100kg grurë dhe thekër, 10% është thekër. Sa kg grurë duhet shtuar që përmbajtja e thekrës të jetë 4% ?
A. 100 kg
B. 115 kg
C. 125 kg
D. 120 kgPyetja 20
Janë dhënë vektorët
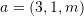 dhe
dhe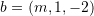 . Sa është vlera e parametrit
. Sa është vlera e parametrit 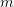 në mënyrë që vektorët të jenë normal ?
në mënyrë që vektorët të jenë normal ?A.
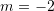
B.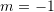
C.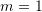
D.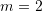
Pyetja 21
Është dhënë
![Rendered by QuickLaTeX.com \displaystyle{x\in\left[\frac{\pi}{4},\frac{5\pi}{4}\right]}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-9aae71582b3e80b4976d2348766fece7_l3.png) . Cili nga inekuacionet është i saktë ?
. Cili nga inekuacionet është i saktë ?A.
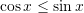
B.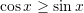
C.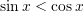
D.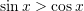
Pyetja 22
Sa është vlera e
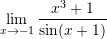 ?
?A. 0
B. 1
C. 2
D. 3Zgjidhje:
Pyetja 23
Në testin e matematikës janë dhënë 20 detyra me numër rendor prej 1 deri 20. Nëse rastësisht zgjedhet një detyrë, atëherë sa është probabiliteti që detyra e zgjedhur rastësisht ka numrin rendor të plotëpjestueshëm me 4 ?
A.

B.

C.
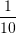
D.
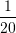
Zgjidhje:
Numrat nga 1-20 qe plotepjestohen me 4 jane
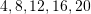
Pra, gjithsej 5 numra
Probabiliteti eshte
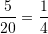
Pyetja 24
Cilat janë zgjidhjet e ekuacionit
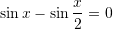 per
per 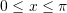 ?
?A.
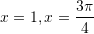
B.
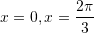
C.
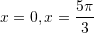
D.
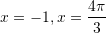
Zgjidhje:
Pyetja 25
Funksioni
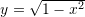 është i përkufizuar për:
është i përkufizuar për:A.
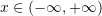
B.![Rendered by QuickLaTeX.com x\in[-1,1]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-74b0788d6e1136048e1fbd86b73972fa_l3.png)
C.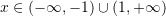
D.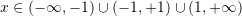
Pyetja 26
Sa është vlera e shumës
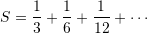 ?
?A.
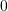
B.

C.

D.

Zgjidhje:
Pyetja 27
Cila është forma trigonometrike e numrit kompleks
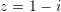 ?
?A.
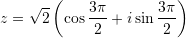
B.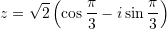
C.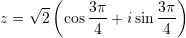
D.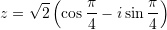
Zgjidhje:
Forma trigonometrike e numrit kompleks eshte
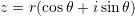 ku
ku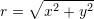 ,
, 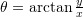
Ne rastin tone
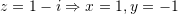
Gjejme modulin

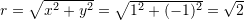
Tani gjejme argumentin
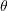
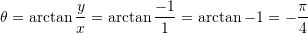
Zevendesojme
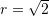 dhe
dhe 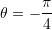 ne
ne 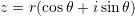
Kemi,
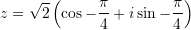
Pyetja 28
Është dhënë funksioni
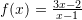 . Sa është
. Sa është 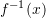
A.
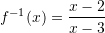
B.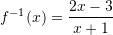
C.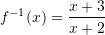
D.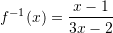
Zgjidhje:
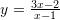
Shumezojme ane per ane me
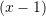
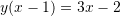
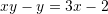
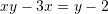
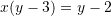
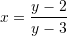
Zevendesojme
 me
me 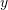
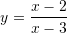
Pra,
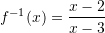
Pyetja 29
Nëse
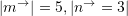 dhe
dhe 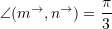 , sa është vlera e shprehjes
, sa është vlera e shprehjes 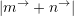 ?
?A. 6
B. 7
C. 8
D. 11Pyetja 30
Cili prej diagrameve vijuese paraqet funksion ,, një – një” ?
A. I
B. II
C. III
D. IVZgjidhje:
Funksioni është një-një nëse
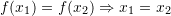 ose nëse
ose nëse 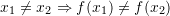 .
.Kështu, kushtin e mësipërm e plotëson diagrami IV.










Zgjidhja e detyes se 7 eshte shume gabim sepse formal a^2 +b^2 nuk eshte e barabart me (a+b)(a+b)
Detyra e 7 mire eshte zgjidhur sepse vlene :
a^2+1/a^2=(a+1/a)(a+1/a)-2.
Si duket nuk po e vereni qeshte -2.
Alma te detyra e 7 a^2+b^2 eshte e barabart me (a+b)(a-b)
E 7ta detyr osht gabim mir e ki alma
#Alma dhe #Habib sa keq qe mendoni qe dini matematike.Gabimet e tilla te juajat nuk lejohen ne matematike e sidomos ne detyra te tilla kaq te lehta.Faton (Y)
Ti jehon mos ma tesh fort
sot e pashe per here te pare
qka pe per her tpar o pal zefi ore
Detyra nr. 10: f(x)=-x^3+3x+2
Pergjigjja e sakt eshte A, sepse ky funksion eshte funksion tek, ku me se lehti verehet nese paraqitet grafiku i fuksionit ne fjale.
Sa per detyren 7, mas lehti ish kon nese e kishit zevendesu sinx=a, dhe 1/sinx=b atehere osht edhe ma leht per me kuptu se a vlen kjo menyr qysh u bo detyra, sepse dihet se (a+b)*(a+b)=(a+b)^2, pra ekuacioni merr formen a^2+b^2=(a+b)^2 ku siq dihet kto dy shprehjet e fundit ne ket barazim nuk jane te barabarta, sepse anes se majte i mungon edhe “2ab”, dmth detyra osht e zgjidhun GABIM!!!
$7 sin(x)= a
a^2+(1/a^2)=[a^2+2a*(1/a)+(1/a^2)]-2a*(1/a)
=[a+(1/a)]^2-2
=(1/2)^2-2
=(1/4)-2
= -7/4