Matematikë, Arsimi Profesional II A 2012
Pyetja 1
Vlera e shprehjes
![Rendered by QuickLaTeX.com \displaystyle{\sqrt[4]{a^5b^7}\sqrt[4]{a^3b^5}}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-acfc21000c4c98c97d757375c433efee_l3.png) është:
është:A.
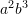
B.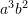
C.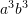
D.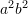
Zgjidhje:
![Rendered by QuickLaTeX.com \displaystyle{\sqrt[4]{a^5b^7}\sqrt[4]{a^3b^5} \Rightarrow \sqrt[4]{a^5b^7a^3b^5} \Rightarrow \sqrt[4]{a^{5+3}b^{7+5}}}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-e613c56b29046d95bbc569ec4f70f14f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\Rightarrow \sqrt[4]{a^{5+3}b^{7+5}} \Rightarrow \sqrt[4]{a^{5+3}b^{7+5}} \Rightarrow \sqrt[4]{a^{8}b^{12}} \Rightarrow a^{2}b^{3}}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-1e52c21192949b141c2a3b2fa263a828_l3.png)
Pyetja 2
Sa trekëndësha mund të ndërtohen me
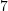 pika jokolineare?
pika jokolineare?A.
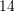
B.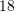
C.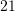
D.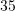
Pyetja 3
Sa është vlera e shprehjes
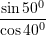 ?
?A.
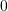
B.
C.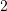
D.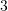
Zgjidhje:
Kendet
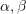 quhen komplementare nese shuma e tyre eshte
quhen komplementare nese shuma e tyre eshte 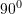
Funksionet trigonometrike te kendeve komplementare jane:
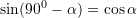
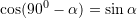
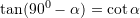
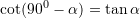
Per kete detyre, shfrytezojme
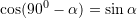
Kemi,
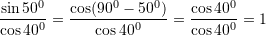
Pyetja 4
Një kënd i trekëndëshit është
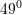 , këndi tjetër është
, këndi tjetër është 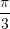 . Sa është këndi i tretë?
. Sa është këndi i tretë?A.
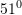
B.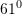
C.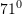
D.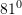
Zgjidhje:
Kendi i pare
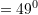
Kendi i dyte
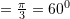
Shuma e kendeve te trekeneshit eshte
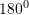
Kendej, kendi i trete=
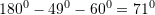
Pyetja 5
Lartësia e ngarkuesit të paraqitur në figurë është:
A. 1.41 m
B. 1.73 m
C. 2.71 m
D. 3.14 mZgjidhje:
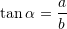
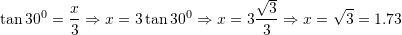
Pyetja 6
Sa është vlera e shprehjes
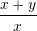 nëse
nëse 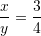
A.

B.

C.

D.

Zgjidhje:
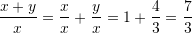
Pyetja 7
Cili është pika simetrike e pikës
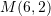 lidhur me drejtëzën e simetrisë
lidhur me drejtëzën e simetrisë 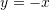 ?
?A.
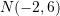
B.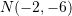
C.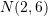
D.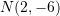
Pyetja 8
Cilat janë gjysmëboshtet e elipsës
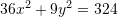 ?
?A.
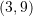
B.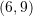
C.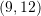
D.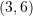
Zgjidhje:
Gjysemboshtet
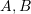 gjinden nga relacioni
gjinden nga relacioni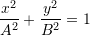
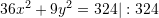
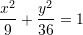
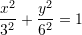
Pra,
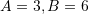
Pyetja 9
Dardhat gjatë tharjes humbin
 e peshës. Sa
e peshës. Sa 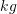 dardha të thara fitohen nga
dardha të thara fitohen nga 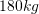 dardha të njoma?
dardha të njoma?A. 40
B. 90
C. 30
D. 140Zgjidhje:
Se pari gjejme sa
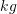 humbin dardhat gjate tharjes
humbin dardhat gjate tharjes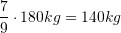
Pra, gjithsej
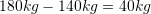 dardha te njoma fitohen.
dardha te njoma fitohen.Pyetja 10
Syprina e trapezit është
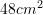 lartësia
lartësia 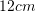 baza e madhe është
baza e madhe është 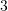 herë më e madhe se baza e vogel. Sa është baza e madhe?
herë më e madhe se baza e vogel. Sa është baza e madhe?A. 2
B. 4
C. 6
D. 8Zgjidhje:
Syprina e trapezit
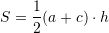
Ne rastin tone,
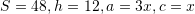
Kemi,
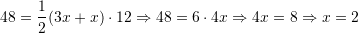
Pra
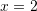 , kerkohet
, kerkohet 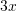
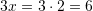
Pyetja 11
Sa është vlera e shprehjes
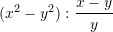 ?
?A.
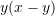
B.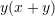
C.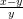
D.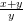
Zgjidhje:
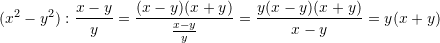
Pyetja 12
Nëse
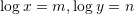 dhe
dhe 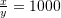 . Sa është vlera
. Sa është vlera  ?
?A. 1
B. 2
C. 3
D. 4Zgjidhje:
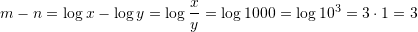
Pyetja 13
Një kulm i shtëpisë ka formën e piramidës së rregullt katërfaqësore me gjatësi të bazës
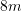 , lartësia e kulmit është
, lartësia e kulmit është 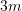 . Sa tjegulla nevojiten për të mbuluar kulmin nëse për
. Sa tjegulla nevojiten për të mbuluar kulmin nëse për 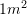 nevojiten
nevojiten 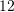 tjegulla?
tjegulla?A. 960 tjegulla
B. 860 tjegulla
C. 760 tjegulla
D. 660 tjegullaPyetja 14
Sa është vlera shprehjës
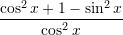 ?
?A. 0
B. 1
C. 2
D. 3Zgjidhje:
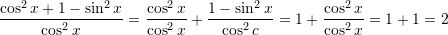
Pyetja 15
Cili zbërthim i përgjigjet trinomit:
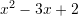 ?
?A.
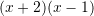
B.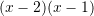
C.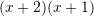
D.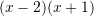
Zgjidhje:
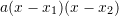
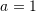
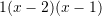
Pyetja 16
Sa zero ka funksioni
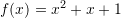 ?
?A. dy zero
B. një zero të dyfishtë
C. tre zero
D. s’ka zeroZgjidhje:
Dallojme tri raste
1. Kur
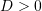 , funksioni ka dy zgjidhje te ndyshme
, funksioni ka dy zgjidhje te ndyshme2. Kur
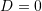 , funksioni ka zgjidhje te dyfishte
, funksioni ka zgjidhje te dyfishte3. Kur
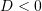 , funksioni ka dy zgjidhje komplekse te konjuguara
, funksioni ka dy zgjidhje komplekse te konjuguaraNe rastin tone,
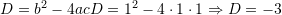
Pra, funksioni ka dy zgjidhje komplekse te konjuguara.
Pyetja 17
Cila është zgjidhja e ekuacinit
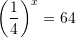 ?
?A.
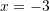
B.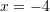
C.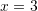
D.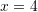
Zgjidhje:
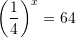
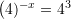
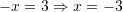
Pyetja 18
Sa është syprina e figurës
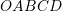 ?
?A. 24
B. 36
C. 48
D. 28Zgjidhje:
Syprinen e figures e njehsojme duke njehsuar syprinat e dy drejtkendeshave dhe nje trekendeshi
Syprina e drejtkendeshit te pare eshte
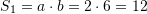
Syprina e drejtkendeshit te dyte eshte
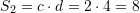
Dhe, syprina e trekendeshit eshte
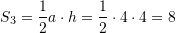
Perfundimisht syprina e figures eshte
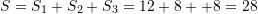
Pyetja 19
Në trekendeshin
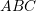 janë dhene
janë dhene 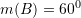 dhe
dhe 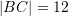 . Sa është brinja
. Sa është brinja 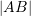 ?
?A. 6
B. 9
C. 12
D. 13Zgjidhje:
Le te jene
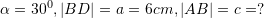
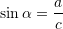
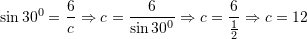
Pyetja 20
Nëse
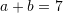 dhe
dhe 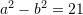 sa është vlera e
sa është vlera e 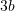 ?
?A.
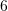
B.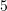
C.
D.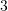
Zgjidhje:
Nga
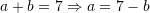
Kemi,
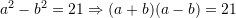
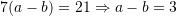
Zëvendësojmë
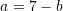
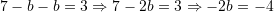
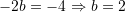
Atëherë
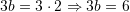
Pyetja 21
Në trekëndëshin ABC, janë dhënë
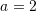 ,
, 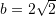 dhe
dhe 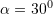 . Zbato teoremen e sinusit dhe trego se cila është vlera e këndit
. Zbato teoremen e sinusit dhe trego se cila është vlera e këndit 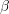 ?
?A.
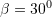
B.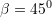
C.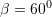
D.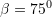
Zgjidhje:
Teorema e Sinusit thotë:
“Në cdo trekëndësh brinjët janë proporcionale me sinuset e këndeve përballë tyre; herësi është i barabartë me diametrin e rrethit të jashtëshkruar në atë trekëndësh.”
Pra,
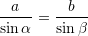
Prej nga,
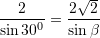
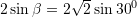
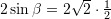
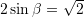
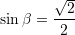

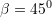
Pyetja 22
Është dhënë funksioni
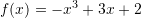 . Cili nga pohimet është i saktë ?
. Cili nga pohimet është i saktë ?A. Funksioni është tek.
B. Funksioni është i tipit racional.
C. Funksioni është gjithkund pozitiv.
D. Funksioni është i tipit polinom.Pyetja 23
Cili prej diagrameve vijuese paraqet funksion ,, një – një” ?
A. I
B. II
C. III
D. IVZgjidhje:
Funksioni është një-një nëse
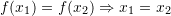 ose nëse
ose nëse 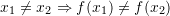 .
.Kështu, kushtin e mësipërm e plotëson diagrami IV.
Pyetja 24
Cili barazim është i saktë ?
A.
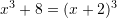
B.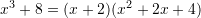
C.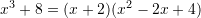
D.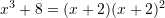
Zgjidhje:
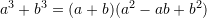
Pyetja 25
Pas racionalizimit, shprehja
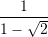 ka formen:
ka formen:A.
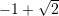
B.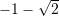
C.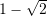
D.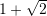
Zgjidhje:
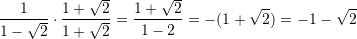










o vlla skoka asnje zgjidhje qetu
te pytja e dyt nuk keni qit zgjidhje as nuk ka te hijezume me te zez kurgjo ?
Edhe te pytja e 13 nuk ka zgjidhje