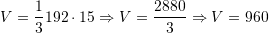Matematikë, Gjimnazi i Përgjithshëm A 2010
Pyetja 1
Cila nga barazitë vijuese është e saktë?
A.
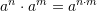
B.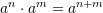
C.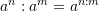
D.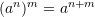
Pyetja 2
Në një rreth janë dhënë 8 pika të ndryshme. Sa trekëndësha me kulme në ato pika mund të formohen ?
A. 52
B. 54
C. 56
D. 58Pyetja 3
Cili nga gjykimet e dhëna është i saktë?
A. p: Nëpër dy pika të dhëna kalojnë dy drejtëza të ndryshme.
B. q: Çdo katërkëndësh ka dy boshte të simetrisë..
C.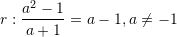 [saktë]
[saktë]
D.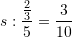
Zgjidhje:
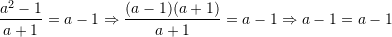
Pyetja 4
Zgjidhjet e ekuacionit kuadratik
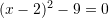 janë:
janë:A.
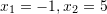
B.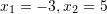
C.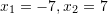
D.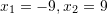
Zgjidhje:
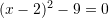
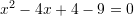
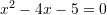
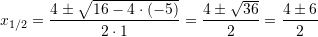
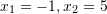
Pyetja 5
Cilat janë zgjidhjet e ekuacionit
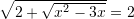
A.
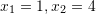
B.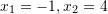
C.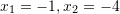
D.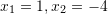
Zgjidhje:
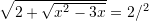
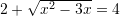
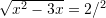
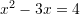
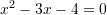
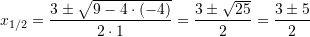
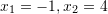
Pyetja 6
Në qoftë se
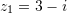 dhe
dhe 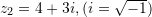 , janë dy numra kompleks, atëherë pjesa reale e numrit kompleks
, janë dy numra kompleks, atëherë pjesa reale e numrit kompleks 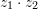 është e barabartë me:
është e barabartë me:A.
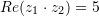
B.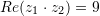
C.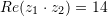
D.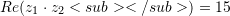
Zgjidhje:
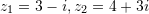 ku
ku 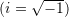
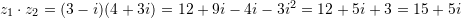
Pyetja 7
Janë dhënë bashkësitë:
![Rendered by QuickLaTeX.com A = [1,6], B = [3, 8]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-6f376f052ff1924f6c68e8793724addc_l3.png) dhe
dhe ![Rendered by QuickLaTeX.com C = [4, 10]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-a400f4fec8c475c08dd90b895badca0a_l3.png) . Sa është
. Sa është 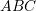 ?
?A.
![Rendered by QuickLaTeX.com A \cap B \cap C = [3,8]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-759440ba0cbd0c05b53b9f46088b6593_l3.png)
B.![Rendered by QuickLaTeX.com A \cap B \cap C = [4,6]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-dbed8f083eadc7b88339eff208ec3bc1_l3.png)
C.![Rendered by QuickLaTeX.com A \cap B \cap C = [3,6]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-f4c363ed6eb6fc846945f92afc2da090_l3.png)
D.![Rendered by QuickLaTeX.com A \cap B \cap C = [4,8]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-947e11d6c4e8d426bb79a900e04914a6_l3.png)
Zgjidhje:
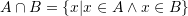
![Rendered by QuickLaTeX.com A\cap B\cap C=[1,6]\cap[3,8]\cap[4,10]=[3,6]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-14c64aeff70f02b10a77bfe355312428_l3.png)
Pyetja 8
Janë dhënë funksionet:
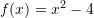 dhe
dhe 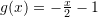 . Sa është
. Sa është 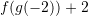 ?
?A. 0
B. -1
C. -2
D. -4Zgjidhje:
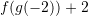
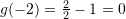
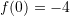
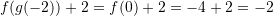
Pyetja 9
Pas thjeshtimit shprehja
![Rendered by QuickLaTeX.com \displaystyle{\left[1-\frac{2ab}{(a+b)^2}\right]:(a^2+b^2)}, a\not= -b](https://testimatures.com/wp-content/ql-cache/quicklatex.com-8c2e82456f4c7fa81102f1606ef9faf2_l3.png) është e barabartë me:
është e barabartë me:A.
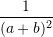
B.
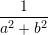
C.
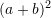
D.
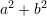
Zgjidhje:
![Rendered by QuickLaTeX.com \displaystyle{\left[1-\frac{2ab}{(a+b)^2}\right]:(a^2+b^2)}, a\not= -b}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-7c474a154b4cef9c67f7c6df99c15194_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\left[\frac{(a+b)^2-2ab}{(a+b)^2}\right]:(a^2+b^2)}}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-a556e0fa674d9ad736aa3c86a88ac044_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\left[\frac{a^2+2ab+b^2-2ab}{(a+b)^2}\right]:(a^2+b^2)}}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-48541e7cc619ecd8636084f2d4d05b6c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\left[\frac{a^2+b^2}{(a+b)^2}\right]:(a^2+b^2)}}](https://testimatures.com/wp-content/ql-cache/quicklatex.com-b69f5c92896c534c273420d5738d9904_l3.png)
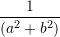
Pyetja 10
Shuma e tre numrave të njëpasnjëshëm është
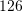 . Cili prej tyre është më i madhi?
. Cili prej tyre është më i madhi?A. 37
B. 39
C. 43
D. 47Zgjidhje:
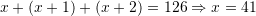
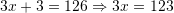
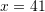
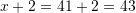
Pyetja 11
Janë dhënë termat
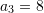 dhe
dhe 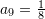 të vargut gjeometrik. Sa është herësi
të vargut gjeometrik. Sa është herësi 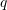 ?
?A.
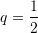 [saktë]
[saktë]B.
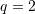
C.
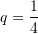
D.
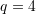
Pyetja 12
Cila është vlera e termit të parë të vargut aritmetik nëse dihet termi i pestë
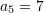 dhe diferenca
dhe diferenca 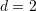 ?
?A.
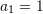
B.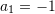
C.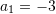
D.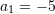
Zgjidhje:
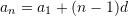
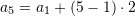
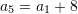
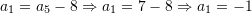
Pyetja 13
Është dhënë trapezi barakrahës me brinjët paralele
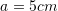 dhe
dhe 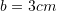 si dhe këndi që formon brinja anësore me brinjën e bazës
si dhe këndi që formon brinja anësore me brinjën e bazës 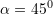 . Sa është lartësia e trapezit ?
. Sa është lartësia e trapezit ?A.
 [saktë]
[saktë]
B.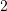
C.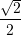
D.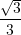
Zgjidhje:
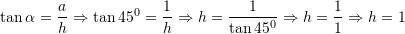
Pyetja 14
Është dhënë shprehja
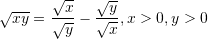 . Sa është vlera e
. Sa është vlera e 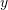 –it ?
–it ?A.
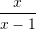
B.
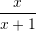
C.
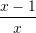
D.
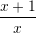
Zgjidhje:
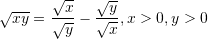
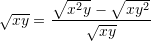
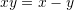
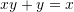
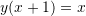
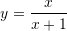
Pyetja 15
Shuma e dy numrave është
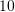 , ndërsa shuma e katrorëve të tyre është
, ndërsa shuma e katrorëve të tyre është 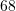 . Cilët janë ata numra?
. Cilët janë ata numra?A.
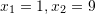
B.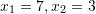
C.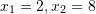 [saktë]
[saktë]
D.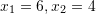
Pyetja 16
Është dhënë
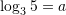 . Në cilin rast është njehsuar saktë
. Në cilin rast është njehsuar saktë 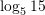 ?
?A.
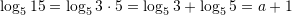
B.
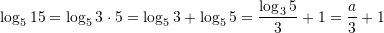
C.
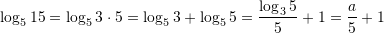
D.
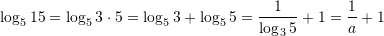 [saktë]
[saktë]Pyetja 17
Në një zarf gjendet numri
 . Për cilin numër është fjala nëse mesatarja e numrave
. Për cilin numër është fjala nëse mesatarja e numrave 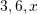 është numri
është numri 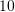 ?
?A.

B.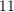
C.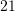
D.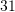
Zgjidhje:
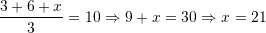
Pyetja 18
Në figurën e dhënë është paraqitur paralelogrami
 dhe gjashtëkëndshi i rregullt
dhe gjashtëkëndshi i rregullt  te cili vlen
te cili vlen ![Rendered by QuickLaTeX.com [AM ] = [MD]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-55e573c655368ecabfa11f73b65f86dd_l3.png) dhe
dhe ![Rendered by QuickLaTeX.com [DQ] = [QC]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-e68ef949b03f2438bd6447cba6fcad07_l3.png) . Sa është gjatësia e
. Sa është gjatësia e ![Rendered by QuickLaTeX.com [AM]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-9a3f0958d0acd22484fe2f3db37a1751_l3.png) , nëse dihet se
, nëse dihet se ![Rendered by QuickLaTeX.com [DB] = 8 cm](https://testimatures.com/wp-content/ql-cache/quicklatex.com-500583191cd8eb9c26bc5026d7193932_l3.png) ?
?A.
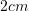
B.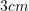
C.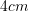
D.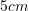
Pyetja 19
Nëse është dhënë
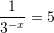 , atëherë sa është
, atëherë sa është 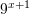 ?
?A.
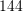
B.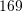
C.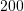
D.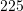
Zgjidhje:
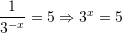
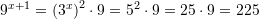
Pyetja 20
Është dhënë piramida e drejtë katërkëndore, baza e të cilës është drejtkëndësh me brinjët
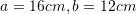 , kurse lartësia
, kurse lartësia 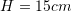 . Sa është vëllimi i piramidës ?
. Sa është vëllimi i piramidës ?A.
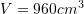
B.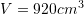
C.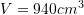
D.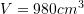
Zgjidhje:
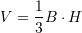
Ne rastin tone,
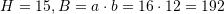
Atehere,