Matematikë, Arsimi Profesional I A 2010
Pyetja 1
Cila nga barazitë vijuese është e saktë?
A.
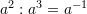 [saktë]
[saktë]
B.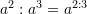
C.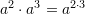
D.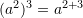
Pyetja 2
Në një rreth janë dhënë 4 pika të ndryshme. Sa trekëndësha me kulme në ato pika mund të formohen ?
A. 2
B. 4
C. 5
D. 6Pyetja 3
Cili nga gjykimet e dhëna është i saktë?
A. p: Nëpër dy pika të dhëna kalojnë dy drejtëza të ndryshme.
B. q: Çdo katërkëndësh ka dy boshte të simetrisë.
C.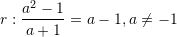 [saktë]
[saktë]
D.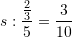
Zgjidhje:
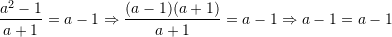
Pyetja 4
Zgjidhjet e ekuacionit kuadratik
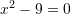 janë:
janë:A.
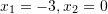
B.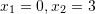
C.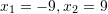
D.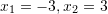
Zgjidhje:
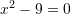
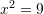
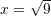
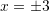
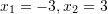
Pyetja 5
Cilat janë zgjidhjet e ekuacionit
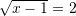
A.
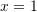
B.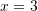
C.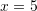
D.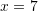
Zgjidhje:
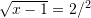
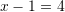
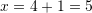
Pyetja 6
Është dhënë funksioni
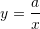 . Cili funksion do të fitohet nëse pika
. Cili funksion do të fitohet nëse pika 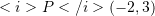 i takon grafikut të funksionit të dhënë?
i takon grafikut të funksionit të dhënë?A.
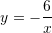
B.
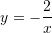
C.
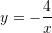
D.
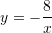
Zgjidhje:
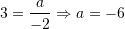
Prandaj,
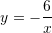
Pyetja 7
Cila është prerja e bashkësive
![Rendered by QuickLaTeX.com A = [1,6]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-986311841b1de3c7c128085d74bcff23_l3.png) dhe
dhe ![Rendered by QuickLaTeX.com B = [3, 8]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-e6e0e1c263bc7217d3afdb1b35bb3d21_l3.png) ?
?A.
![Rendered by QuickLaTeX.com A \cap B = [1,3]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-9a9059190c3cfa21c96f7644cc0b779b_l3.png)
B.![Rendered by QuickLaTeX.com A \cap B = [3,8]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-834cef2e621cfbd20bd165c8e971528f_l3.png)
C.![Rendered by QuickLaTeX.com A \cap B = [3,6]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-c0b120f2bbe8fb08ddf262f1c2cfffa8_l3.png)
D.![Rendered by QuickLaTeX.com A \cap B = [6,8]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-1aaa8b5eb8ff1f3d3f0b33c9d6f242a6_l3.png)
Zgjidhje:
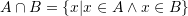
![Rendered by QuickLaTeX.com A\cap B\cap C=[1,6]\cap[3,8]=[3,6]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-f8f1fea9e75de5d2e0e3af87c4b03eaa_l3.png)
Pyetja 8
Janë dhënë funksionet:
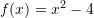 dhe
dhe 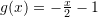 . Sa është
. Sa është 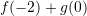 ?
?A. 0
B. -1
C. -2
D. -4Zgjidhje:
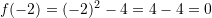
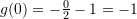
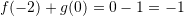
Pyetja 9
Sa është 5% e numrit 20 ?
A.

B.

C.

D.
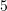
Zgjidhje:
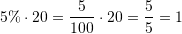
Pyetja 10
Shuma e tre numrave të njëpasnjëshëm është
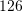 . Cili prej tyre është më i madhi?
. Cili prej tyre është më i madhi?A. 37
B. 39
C. 43
D. 47Zgjidhje:
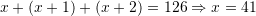
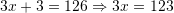
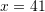
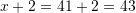
Pyetja 11
Janë dhënë këndet
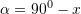 dhe
dhe 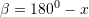 . Sa është vlera e këndit
. Sa është vlera e këndit  nëse
nëse 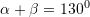 ? ?
? ?A.
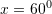
B.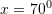 [saktë]
[saktë]
C.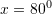
D.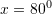
Zgjidhje:
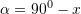
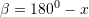
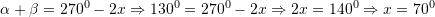
Pyetja 12
Në cilin rast shprehja
![Rendered by QuickLaTeX.com 15 -12 : 3 + 4 - [-(-2 ⋅ 4 + 1)]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-a3959c3b82acb5638784618ed9ea4a3a_l3.png) është njehsuar saktë?
është njehsuar saktë?A.
![Rendered by QuickLaTeX.com 15 -12 : 3 + 4 - [-(-2 ⋅ 4 + 1)] = 3 : 3 + 4 + 8 -1 = 1 +12 -1 = 12](https://testimatures.com/wp-content/ql-cache/quicklatex.com-6e6dbabcc136ba99af9bbb48950f4f92_l3.png)
B.![Rendered by QuickLaTeX.com 15 -12 : 3 + 4 - [-(-2 ⋅ 4 + 1)] = 15 - 4 + 4 - [-8 -1] = 15 - 9 = 6](https://testimatures.com/wp-content/ql-cache/quicklatex.com-273d5f416d18f74195b8f310cf9e034a_l3.png)
C.![Rendered by QuickLaTeX.com 15 - 12 : 3 + 4 - [-(-2 ⋅ 4 + 1)] = 15 - 4 + 4 - [8 - 1] = 15 - 7 = 8](https://testimatures.com/wp-content/ql-cache/quicklatex.com-498c0afe8e9f5ffc8f65d727821d10af_l3.png) [saktë]
[saktë]
D.![Rendered by QuickLaTeX.com 15 -12 : 3 + 4 - [-(-2 ⋅ 4 +1)] = 3 + 4 + [-8 +1] = 7 + [-7] = 7 - 7 = 0](https://testimatures.com/wp-content/ql-cache/quicklatex.com-b3681760c185746385a6f127f7e95759_l3.png)
Pyetja 13
Është dhënë shprehja
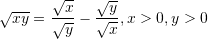 . Sa është vlera e
. Sa është vlera e 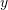 –it ?
–it ?A.
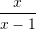
B.
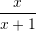
C.
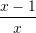
D.
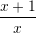
Zgjidhje:
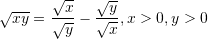
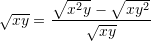
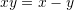
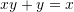
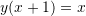
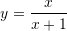
Pyetja 14
Duke ditur se vlen barazia
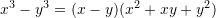 , tregoni se cila barazi është e saktë?
, tregoni se cila barazi është e saktë?A.
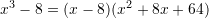
B.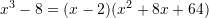
C.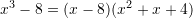
D.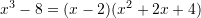
Zgjidhje:
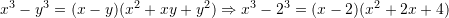
Pyetja 15
Shuma e dy numrave është
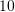 , ndërsa shuma e katrorëve të tyre është
, ndërsa shuma e katrorëve të tyre është 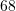 . Cilët janë ata numra?
. Cilët janë ata numra?A.
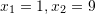
B.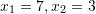
C.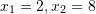 [saktë]
[saktë]
D.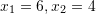
Pyetja 16
Cili pohim është i saktë për funksionin y = x2 + 4x ?
A. Është funksion periodik.
B. Ka minimum në pikën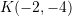 .
.
C. Është pozitiv në intervalin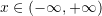 .
.
D. E pret boshtin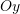 në dy pika.
në dy pika.Pyetja 17
Në një zarf gjendet numri
 . Për cilin numër është fjala nëse mesatarja e numrave
. Për cilin numër është fjala nëse mesatarja e numrave 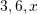 është numri
është numri 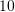 ?
?A.

B.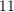
C.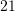
D.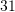
Zgjidhje:
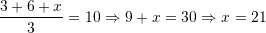
Pyetja 18
Në figurën e dhënë është paraqitur paralelogrami
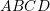 dhe gjashtëkëndshi i rregullt
dhe gjashtëkëndshi i rregullt 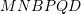 te cili vlen
te cili vlen ![Rendered by QuickLaTeX.com [AM ] = [MD]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-55e573c655368ecabfa11f73b65f86dd_l3.png) dhe
dhe ![Rendered by QuickLaTeX.com [DQ] = [QC]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-e68ef949b03f2438bd6447cba6fcad07_l3.png) . Sa është gjatësia e
. Sa është gjatësia e ![Rendered by QuickLaTeX.com [AM]](https://testimatures.com/wp-content/ql-cache/quicklatex.com-9a3f0958d0acd22484fe2f3db37a1751_l3.png) , nëse dihet se
, nëse dihet se ![Rendered by QuickLaTeX.com [DB] = 8 cm](https://testimatures.com/wp-content/ql-cache/quicklatex.com-500583191cd8eb9c26bc5026d7193932_l3.png) ?
?A.
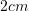
B.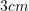
C.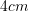
D.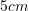
Pyetja 19
Numri i kundërt i numrit a, (a ≠ 0) në lidhje me veprimin e shumëzimit është numri:
A.
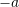
B.

C.
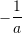
D.
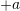
Pyetja 20
Është dhënë piramida e drejtë katërkëndore, baza e të cilës është drejtkëndësh me brinjët
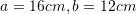 , kurse lartësia
, kurse lartësia 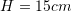 . Sa është vëllimi i piramidës ?
. Sa është vëllimi i piramidës ?A.
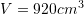
B.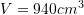
C.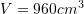
D.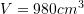
Zgjidhje:
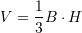
Ne rastin tone,
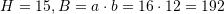
Atehere,
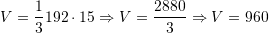

Bravo 😛